Triângulo

O que é um triângulo?

Os triângulos ou trígonos são figuras geométricas planas e básicas que têm três lados em contato uns com os outros em pontos comuns chamados vértices. Seu nome vem do fato de possuir três ângulos internos ou internos, formados por cada par de linhas em contato no mesmo vértice.

Essas figuras geométricas são nomeadas e classificadas de acordo com a forma de seus lados e o tipo de ângulo que fazem. No entanto, seus lados são sempre três e a soma de todos os seus ângulos sempre dará 180 ° .

Os triângulos são estudados pela humanidade desde tempos imemoriais, pois foram associados ao divino, aos mistérios e à magia. Portanto, é possível encontrá-los em muitos símbolos ocultos ( Maçonaria , Bruxaria, Cabala, etc.) e em tradições religiosas . Seu número associado, três (3), numerologicamente alude ao mistério da concepção e da própria vida.

Na história do triângulo, a antiguidade grega merece um lugar de destaque. O grego Pitágoras (c. 569 – c. 475 aC) propôs seu famoso teorema para triângulos retângulos, que afirma que o quadrado da hipotenusa é igual à soma do quadrado das pernas.

Veja também: Trigonometria

Propriedades do triângulo

A propriedade mais óbvia dos triângulos são seus três lados, três vértices e três ângulos , que podem ser semelhantes ou totalmente diferentes uns dos outros. Os triângulos são os polígonos mais simples que existem e não têm diagonal , pois com quaisquer três pontos não alinhados é possível formar um triângulo.

Na verdade, qualquer outro polígono pode ser dividido em um conjunto ordenado de triângulos, no que é conhecido como triangulação , portanto, o estudo de triângulos é fundamental para a geometria.

Além disso, os triângulos são sempre convexos , nunca côncavos, pois seus ângulos nunca podem exceder 180 ° (ou π radianos).

Elementos triangulares

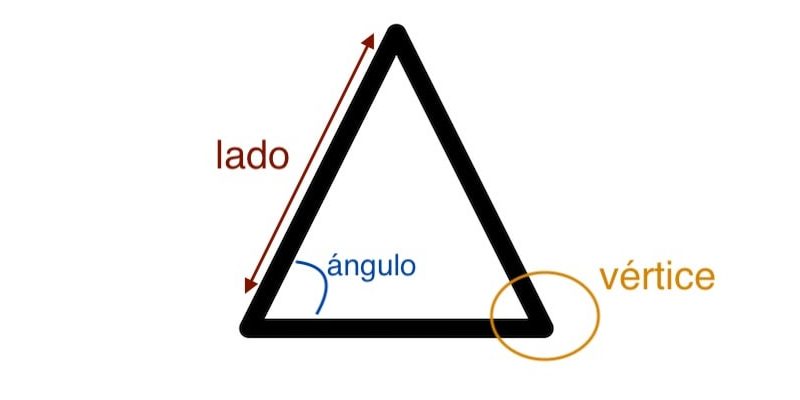
Os triângulos são compostos de vários elementos, muitos dos quais já mencionamos:

• Vértices. Estes são os pontos que definem um triângulo ao unir dois deles com uma linha reta. Assim, se tivermos os pontos A, B e C, juntá-los às retas AB, BC e CA nos dará um triângulo como resultado. Além disso, os vértices estão no lado oposto dos ângulos internos do polígono.
• Lados. É o nome dado a cada uma das linhas que unem os vértices de um triângulo, delimitando a figura (o interior do exterior).
• Ângulos . Cada dois lados de um triângulo forma em seu vértice comum algum tipo de ângulo, que é chamado de ângulo interno, pois está voltado para o lado interno do polígono. Esses ângulos são, como os lados e vértices, sempre três.

Tipos de triângulo

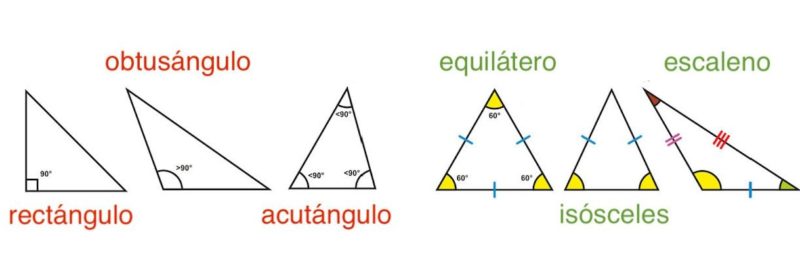
Existem duas classificações principais de triângulos:

• De acordo com seus lados. Dependendo da relação entre seus três lados diferentes, um triângulo pode ser:
  • Equilátero. Quando seus três lados têm exatamente o mesmo comprimento .
  • Isósceles. Quando dois de seus lados têm o mesmo comprimento e o terceiro, diferente.
  • Escaleno. Quando seus três lados têm comprimentos diferentes um do outro.
• De acordo com seus ângulos. Em vez disso, dependendo da abertura de seus ângulos, podemos falar de triângulos:
  • Retângulos. Apresentam um ângulo reto (90 °) formado por dois lados semelhantes (pernas) e opostos ao terceiro (hipotenusa).
  • Ângulos oblíquos. Aqueles que não apresentam nenhum ângulo reto, e que por sua vez podem ser:
    • Ângulos contundentes. Quando um de seus ângulos internos é obtuso (maior que 90 °) e os outros dois agudos (menor que 90 °).
    • Ângulos agudos. Quando seus três ângulos internos são agudos (menos de 90 °).

Essas duas classificações podem ser combinadas, permitindo-nos falar de triângulos retângulos isósceles, triângulos agudos escalenos, etc.

Perímetro de um triângulo

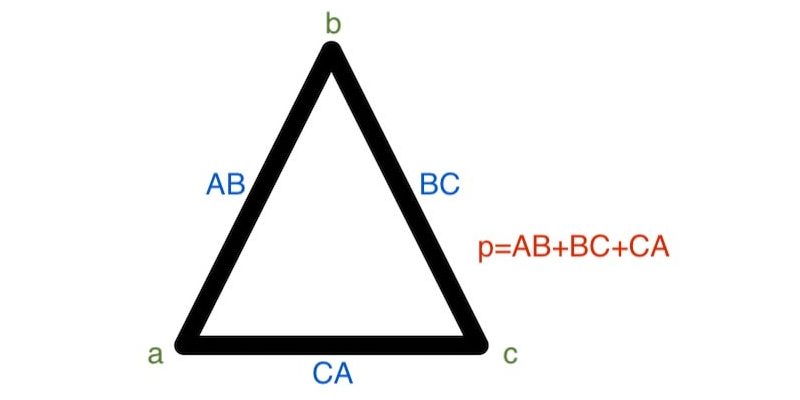
O perímetro de um triângulo é a soma dos comprimentos de seus lados e geralmente é denotado pela letra p ou 2s . A equação para determinar o perímetro de um determinado triângulo ABC é:

p = AB + BC + AC .

Por exemplo: um triângulo cujos lados são 5cm, 5cm e 10cm terá um perímetro de 20cm.

Área de um triângulo

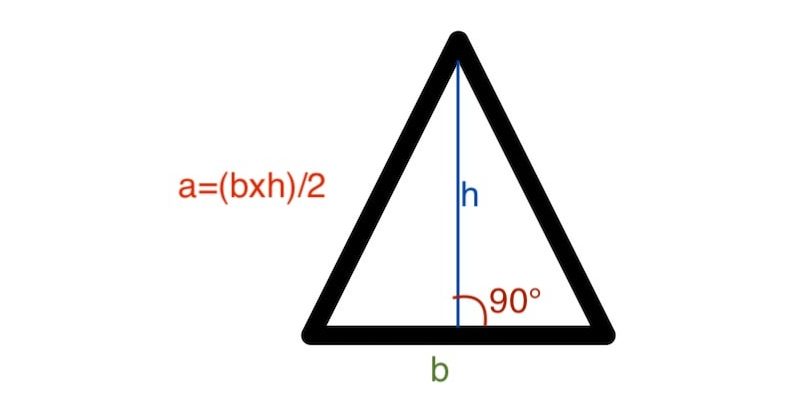
A área de um triângulo (a) é o espaço interior delimitado por seus três lados . Pode ser calculado conhecendo sua base (b) e sua altura (h), de acordo com a fórmula:

a = (bh) / 2 .

A área é medida em unidades de comprimento ao quadrado (cm ² , m ² , km ² , etc.)

A base de um triângulo é o lado em que a figura “repousa”, geralmente a parte inferior. Em vez disso, para encontrar a altura de um triângulo, precisamos traçar uma linha do vértice oposto à base , ou seja, o ângulo superior. Essa linha deve formar um ângulo reto com a base.

Assim, por exemplo, tendo um triângulo isósceles com lados: 11 cm, 11 cm e 7,5 cm, podemos calcular sua altura (7 cm) e então aplicar a fórmula: a = (11 cm x 7 cm) / 2, que dá um resultado de 38,5 cm ² .

Outras figuras geométricas

Outras figuras geométricas bidimensionais importantes são:

• O quadrado. Polígonos com quatro lados perfeitamente iguais, ancestrais bidimensionais do cubo.
• O retângulo. Se tomarmos um quadrado e alongarmos dois de seus lados opostos, obteremos uma figura composta por quatro linhas: duas iguais e duas diferentes (mas iguais entre si). Isso é um retângulo.
• O circulo. Todos conhecemos o círculo, uma das formas mais simples da geometria e que consiste numa linha curva contínua que regressa ao ponto de partida traçando 360 ° de circunferência.

Continue com: Matemática