Explicamos o que é adição ou adição em matemática, sua história, propriedades e exemplos. Além disso, métodos para adicionar frações.

Qual é a soma?
A adição ou adição é uma operação matemática fundamental, que consiste na incorporação de novos elementos a um conjunto numérico , ou seja, a fusão de dois números para obter um novo, que expressa o valor total dos dois anteriores. A adição é o princípio fundamental com o qual aprendemos a nos conectar com os números, já que o simples fato de contar um por um (1, 2, 3, 4 …) envolve somar 1 (1 + 0, 1 + 1, 1 + 2, 1 + 3 …).
A adição é uma operação do tipo aritmético, que permite combinar números de diferentes tipos : naturais , inteiros , frações, reais, racionais, irracionais e complexos, bem como estruturas a eles associadas, como espaços vetoriais ou matrizes. Na álgebra moderna , é representado pelo símbolo + , inserido entre os elementos a serem adicionados e expresso verbalmente como “mais”: “1 + 1 = 2” é lido como “um mais um é igual a dois”.
Por outro lado, os elementos a serem somados são conhecidos como “adendos”, e o número obtido ao final é denominado “resultado”.
Pode te ajudar: Matemática
História da soma
A adição é uma das operações matemáticas mais antigas e básicas conhecidas. Pensa-se que o ser humano neolítico já tratava dos princípios matemáticos elementares , entre os quais estariam necessariamente a adição e a subtração, uma vez que essas operações são fáceis de evidenciar face aos fornecimentos agrícolas que aumentavam e diminuíam de acordo com a época do ano.
No entanto, o estudo da adição e sua aplicação aos números naturais e fracionários começou com os antigos egípcios e continuou a se desenvolver de maneiras mais complexas com os babilônios, especialmente com os chineses e hindus, que foram os primeiros a adicionar números. . Mas foi só no Renascimento que o boom bancário impôs a soma de decimais e logaritmos vulgares.
Propriedades da soma
A adição como operação matemática possui um conjunto de propriedades, que são:
- Propriedade comutativa . Estabelece que a ordem dos adendos não altera o resultado, ou seja, que a + b é exatamente igual a b + a, e em ambos os casos obtém-se o mesmo resultado.
- Propriedade associativa . Estabelece que ao adicionar três ou mais elementos, é possível agrupar dois deles para resolvê-los primeiro, independentemente de quais sejam, sem alterar o resultado final. Ou seja, se quisermos adicionar a + b + c, podemos escolher duas maneiras: (a + b) + c ou a + (b + c), sem afetar o resultado de forma alguma.
- Propriedade de identidade . Estabelece que zero é um elemento neutro na operação, portanto, somar com qualquer outro número sempre resultará neste último número: a + 0 = a.
- Fechando propriedade . Estabelece que o resultado de uma soma pertencerá sempre ao mesmo conjunto numérico de adendos, desde que estes por sua vez compartilhem o mesmo conjunto. Ou seja, se os adendos aeb pertencem a N (natural), Z (inteiros), Q (irracional), R (real) ou C (complexo), o resultado da soma também pertencerá ao mesmo conjunto.
Exemplos de adição
Aqui estão alguns exemplos de adição simples:
- Uma mulher tem quatro flores, mas é seu aniversário e ela recebe mais oito. Quantas flores ele tem no final do dia? 4 flores + 8 flores = 12 flores.
- Um pastor tem 15 ovelhas, enquanto um colega dele tem 13. Se eles decidirem fundir seus rebanhos, quantas ovelhas terão ao todo? 15 ovelhas + 13 ovelhas = 28 ovelhas.
- Uma macieira dá ao seu dono 5 maçãs por mês. Quantas maçãs ele terá ao final de um ano? Como um ano é 12 meses, devemos somar 5 doze vezes, aplicando a propriedade associativa: (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + (5 + 5) + ( 5 + 5) = (10 + 10) + (10 + 10) + (10 + 10) = 20 + 20 + 20 = 60 maçãs em um ano.
Soma das frações
Ao adicionar frações, existem diferentes métodos que podemos aplicar para obter o resultado, consoante se trate de frações adequadas, impróprias e mistas.
- Método de adição de frações com o mesmo denominador . Este é o caso mais simples, em que simplesmente somamos os numeradores e mantemos o mesmo denominador. Por exemplo:
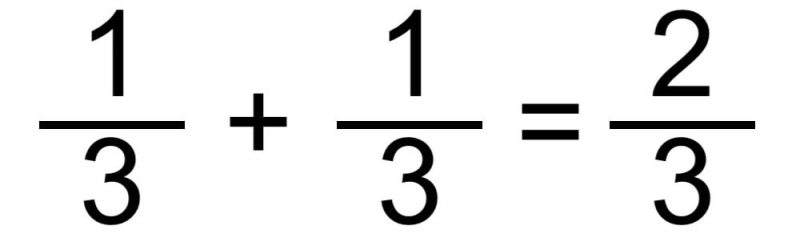
ou
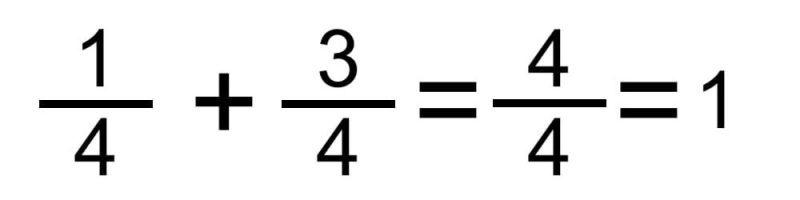
- Método borboleta . Este método nos permite adicionar qualquer tipo de frações com diferentes denominadores, simplesmente multiplicando o numerador do primeiro pelo denominador do segundo e vice-versa, e depois somar os produtos (para obter o numerador) e, em seguida, multiplicar os denominadores para obter o denominador da fração final. Uma vez que essas operações tenham sido realizadas, muitas vezes teremos que reduzir o resultado. Por exemplo:
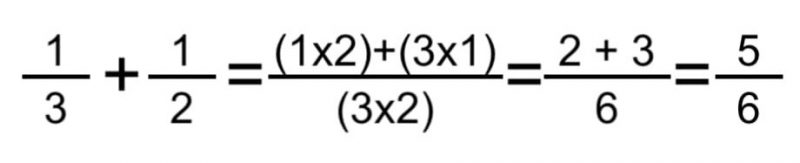
- Método para adicionar três frações . Nesse caso, simplesmente adicionamos os dois primeiros e adicionamos o último ao resultado, aplicando o método anterior e reduzindo ou simplificando o resultado se necessário. Por exemplo:
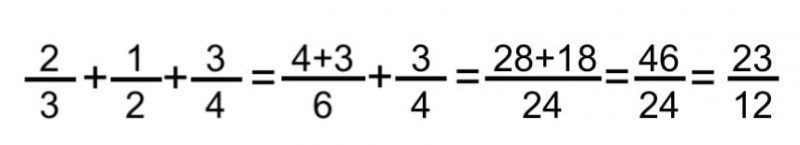
Continue com: Planilha