Explicamos o que é álgebra, sua história, ramos e para que serve. Além disso, linguagem e expressões algébricas.

O que é álgebra?
A álgebra é um dos principais ramos da matemática . Seu objeto de estudo são estruturas abstratas operando em padrões fixos, dentro dos quais geralmente existem mais do que números e operações aritméticas: também letras, que representam operações concretas, variáveis , incógnitas ou coeficientes.
Simplificando, é o ramo da matemática que lida com operações com e entre símbolos , geralmente representados por letras. Seu nome vem do árabe al-ŷabr (“reintegração” ou “recomposição”).
A álgebra é um dos ramos da matemática com maiores aplicações. Permite representar os problemas formais da vida cotidiana. Por exemplo, equações e variáveis algébricas permitem calcular proporções desconhecidas .
A lógica , o reconhecimento de padrões e o raciocínio indutivo e dedutivo são algumas das competências mentais exigidas, que promove e desenvolve.
Veja também: Pensamento matemático
História da álgebra

A álgebra nasceu na cultura árabe, por volta de 820 DC. C. , data em que o primeiro tratado sobre o assunto foi publicado: Al-kitāb al-mukhtaṣar fī ḥisāb al-ŷarabi waˀl-muqābala , ou seja, “Compêndio de cálculo por reintegração e comparação”, obra do matemático e astrônomo persa Muhammad ibn Musa al-Jwarizmi, conhecido como Al Juarismi.
Lá, o sábio ofereceu a solução sistemática de equações lineares e quadráticas, usando operações simbólicas. Esses métodos foram posteriormente desenvolvidos na matemática do Islã medieval e tornaram a álgebra uma disciplina matemática independente, ao lado da aritmética e da geometria.
Esses estudos acabaram chegando ao Ocidente. Graças a eles, a álgebra abstrata surgiu no século XIX , a partir da consolidação de números complexos durante os séculos anteriores, fruto de pensadores como Gabriel Cramer (1704-1752), Leonhard Euler (1707-1783) e Adrien-Marie Legendre ( 1752-1833).
Para que serve a álgebra?
A álgebra é extremamente útil no campo da matemática, mas também tem grandes aplicações na vida cotidiana. Permite realizar orçamentos , faturas, cálculos de custos , benefícios e lucros .
Além disso, outras operações importantes em contabilidade , administração e até engenharia, baseiam-se em cálculos algébricos que tratam de uma ou mais variáveis, expressando-as em relações lógicas e padrões detectáveis.
O uso da álgebra permite que os indivíduos lidem melhor com conceitos complexos e abstratos , expressando-os de forma mais simples e ordenada por meio da notação algébrica.
Ramos da álgebra
As principais ramificações da álgebra são duas:
- Álgebra elementar. Como o próprio nome indica, compreende os preceitos mais básicos da matéria, introduzindo nas operações aritméticas uma série de letras (símbolos) que representam quantidades ou relações desconhecidas. Este é, fundamentalmente, o tratamento de equações e variáveis, incógnitas, coeficientes, índices ou raízes.
- Álgebra abstrata. Também chamado de álgebra moderna, representa um grau de complexidade maior do que o elementar, pois se dedica ao estudo de estruturas algébricas ou sistemas algébricos, que são conjuntos de operações que podem ser associados a elementos de um grupo de padrões reconhecíveis.
Linguagem algébrica
A álgebra requer, acima de tudo, uma forma própria de nomear suas sentenças, diferente da linguagem aritmética (composta apenas por números e símbolos), apelando para relações, variáveis e operações tradicionais e complexas.
É uma linguagem mais sintética do que a aritmética, que permite expressar relações gerais por meio de frases curtas . Também nos permite incluir no padrão formal aqueles termos que ainda não conhecemos (as variáveis), mas cuja ligação com o resto é conhecida.
É assim que surgem as equações, por exemplo, cuja forma de resolução envolve reorganizar os termos algébricos para “limpar” o desconhecido.
Expressões algébricas
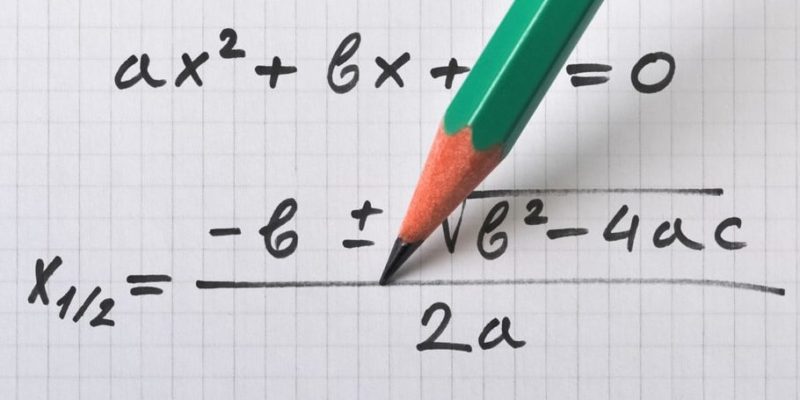
Expressões algébricas são a maneira de escrever linguagem algébrica . Neles reconheceremos números e letras (variáveis), mas também outros tipos de sinais e disposições, como coeficientes (números antes de uma variável), graus (sobrescritos) e os sinais aritméticos usuais. Em linhas gerais, as expressões algébricas podem ser classificadas em duas:
- Monômios. Uma única expressão algébrica, que contém em si todas as informações necessárias para resolvê-la. Por exemplo: 6X 2 + 32y 4 .
- Polinômios. Strings de expressões algébricas, ou seja, strings de monômios, que têm um significado global e devem ser resolvidos juntos. Por exemplo: 3n5y 3 + 23n 5 y8z 3 – π 2 3n – 22 + 26n 4 .
Continue com: Geometria Analítica